Che cos'è un'alimentazione elettrica?

L'uomo moderno incontra costantemente l'elettricità nella vita di tutti i giorni e al lavoro, utilizza dispositivi che consumano corrente elettrica e dispositivi che la generano. Quando lavori con loro, dovresti sempre tenere conto delle loro capacità inerenti alle caratteristiche tecniche.

Uno dei principali indicatori di qualsiasi dispositivo elettrico è una quantità fisica come energia elettrica... È consuetudine chiamare l'intensità o la velocità di generazione, trasmissione o conversione dell'elettricità in altri tipi di energia, ad esempio calore, luce, meccanico.

Il trasporto o il trasferimento di grandi quantità di energia elettrica per scopi industriali è effettuato secondo linee elettriche ad alta tensione.

Trasformazione energia elettrica viene effettuato nelle sottostazioni di trasformazione.

Il consumo di elettricità si verifica in dispositivi domestici e industriali per vari scopi. Uno dei loro tipi comuni è lampade a incandescenza di varie potenze.

La potenza elettrica di generatori, linee elettriche e consumatori nei circuiti CC e CA ha lo stesso significato fisico, che viene espresso simultaneamente in rapporti diversi a seconda della forma dei segnali compositi. Per definire i modelli generali, nozioni di valori istantanei... Sottolineano ancora una volta la dipendenza della velocità di trasformazione dell'elettricità dal tempo.

Determinazione della potenza elettrica istantanea

Nell'ingegneria elettrica teorica, al fine di derivare le relazioni di base tra corrente, tensione e potenza, vengono utilizzate le loro immagini sotto forma di valori istantanei, che sono fissati in un determinato momento.

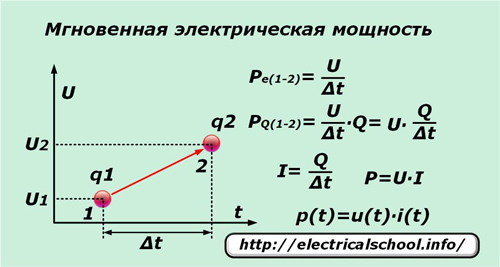
Se in un periodo di tempo molto breve ∆t una singola carica elementare q sotto l'influenza della tensione U si sposta dal punto «1» al punto «2», allora compie un lavoro pari alla differenza di potenziale tra questi punti. Dividendolo per l'intervallo di tempo ∆t si ottiene l'espressione della potenza istantanea per unità di carica Pe (1-2).

Poiché non solo la singola carica si muove sotto l'azione della tensione applicata, ma anche tutte quelle adiacenti che sono sotto l'influenza di questa forza, il cui numero è convenientemente rappresentato dal numero Q, allora il valore istantaneo della potenza PQ (1-2) può essere scritto per loro.

Dopo aver eseguito semplici trasformazioni, otteniamo l'espressione per la potenza P e la dipendenza del suo valore istantaneo p (t) dalle componenti del prodotto della corrente istantanea i (t) e della tensione u (t).

Determinazione della potenza elettrica costante

v Circuiti CC l'entità della caduta di tensione nella sezione del circuito e la corrente che lo attraversa non cambia e rimane stabile, pari ai valori istantanei.Pertanto, la potenza in questo circuito può essere determinata moltiplicando questi valori o dividendo l'opera perfetta A per il periodo della sua esecuzione, come mostrato nella figura esplicativa.

Determinazione della potenza elettrica in corrente alternata

Le leggi della variazione sinusoidale delle correnti e delle tensioni trasmesse attraverso le reti elettriche impongono la loro influenza sull'espressione della potenza in tali circuiti. Qui entra in gioco la potenza apparente, descritta dal triangolo di potenza e composta da componenti attive e reattive.

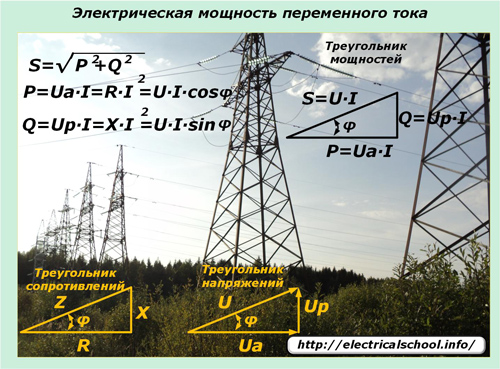
Una corrente elettrica sinusoidale quando passa attraverso linee elettriche con tipi misti di carichi in tutte le sezioni non cambia la forma della sua armonica e la caduta di tensione ai carichi reattivi si sposta in fase in una certa direzione. Le espressioni del valore del momento aiutano a comprendere l'effetto dei carichi applicati sulla variazione di potenza nel circuito e sulla sua direzione.

Allo stesso tempo, prestare immediatamente attenzione al fatto che la direzione del flusso di corrente dal generatore al consumatore e la potenza trasmessa attraverso il circuito creato sono cose completamente diverse, che in alcuni casi potrebbero non solo non coincidere, ma anche essere diretti in direzioni opposte.

Considera queste relazioni nella loro manifestazione ideale e pura per diversi tipi di carichi:

• attivo;

• capacitivo;

• induttivo.

Dissipazione di potenza del carico attivo

Supponiamo che il generatore produca una tensione sinusoidale ideale u che viene applicata alla resistenza puramente attiva del circuito. L'amperometro A e il voltmetro V misurano la corrente I e la tensione U ogni volta t.

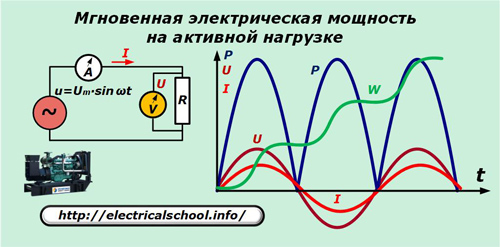
Il grafico mostra che le sinusoidi della corrente e la caduta di tensione attraverso la resistenza attiva coincidono in frequenza e fase, producendo le stesse oscillazioni. La forza espressa dal loro prodotto oscilla al doppio della frequenza e rimane sempre positiva.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

Se andiamo all'espressione tensione di esercizio, allora otteniamo: p = P ∙ (1-cos2ωt).

Integreremo quindi la potenza sul periodo di un'oscillazione T e potremo notare che il guadagno di energia ∆W durante questo intervallo aumenta. Nel tempo la resistenza continua a consumare nuove porzioni di elettricità, come mostrato nel grafico.

Con carichi reattivi, le caratteristiche del consumo di energia sono diverse, hanno una forma diversa.

Dissipazione di potenza capacitiva

Nel circuito elettrico del generatore, sostituire l'elemento resistivo con un condensatore di capacità C.

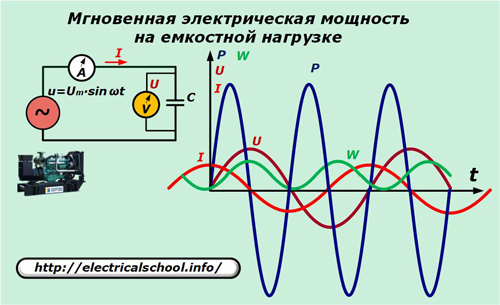
La relazione tra la corrente e la caduta di tensione nella capacità è espressa dal rapporto: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

Moltiplichiamo i valori delle espressioni istantanee di corrente con tensione e otteniamo il valore della potenza consumata dal carico capacitivo.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt.

Qui puoi vedere che la potenza fluttua intorno allo zero al doppio della frequenza della tensione applicata. Il suo valore totale per il periodo armonico, così come il guadagno di energia, è zero.

Ciò significa che l'energia si muove lungo il circuito chiuso del circuito in entrambe le direzioni, ma non funziona.Tale fatto è spiegato dal fatto che quando la tensione della sorgente aumenta in valore assoluto, la potenza è positiva e il flusso di energia attraverso il circuito viene diretto al contenitore, dove viene accumulata l'energia.

Dopo che la tensione è passata alla sezione armonica discendente, l'energia viene restituita dal condensatore al circuito alla sorgente. Nessun lavoro utile viene svolto in entrambi i processi.

Dissipazione di potenza in un carico induttivo

Ora, nel circuito di alimentazione, sostituisci il condensatore con l'induttanza L.

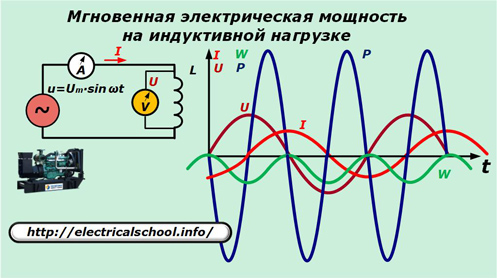
Qui la corrente attraverso l'induttanza è espressa dal rapporto:

io = 1 / L∫udt = -Um / ωL ∙ cosωt.

Quindi otteniamo

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ (2ХL) ∙ sin2ωt.

Le espressioni risultanti ci permettono di vedere la natura del cambiamento di direzione della potenza e dell'aumento di energia sull'induttanza, che compie le stesse oscillazioni inutili per compiere lavoro, come sulla capacità.

La potenza rilasciata nei carichi reattivi è chiamata componente reattiva. In condizioni ideali, quando i fili di collegamento non hanno resistenza attiva, appare innocuo e non provoca alcun danno. Ma in condizioni di potenza reale, transitori periodici e fluttuazioni di potenza reattiva provocano il riscaldamento di tutti gli elementi attivi, compresi i cavi di collegamento, per i quali viene consumata una certa energia e il valore della piena potenza applicata della sorgente diminuisce.

La principale differenza tra la componente reattiva della potenza è che non svolge affatto un lavoro utile, ma porta a perdite di energia elettrica e carichi eccessivi sulle apparecchiature, che sono particolarmente pericolose in situazioni critiche.

Per questi motivi, per eliminare l'influenza della potenza reattiva, esp sistemi tecnici per la sua compensazione.

Distribuzione di potenza a carico misto

Ad esempio, utilizziamo il carico di un generatore con una caratteristica capacitiva attiva.

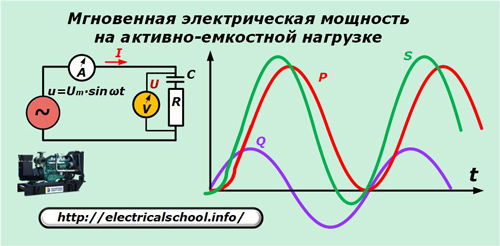
Per semplificare il quadro, le sinusoidi di correnti e tensioni non sono mostrate nel grafico dato, ma va tenuto presente che con una natura attiva-capacitiva del carico, il vettore corrente anticipa la tensione.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

Dopo le trasformazioni otteniamo: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

Questi due termini nell'ultima espressione sono le componenti attiva e reattiva della potenza apparente istantanea. Solo il primo di questi funziona in modo utile.

Strumenti per la misurazione della potenza

Per analizzare il consumo di elettricità e calcolarlo, vengono utilizzati dispositivi di misurazione, che sono stati a lungo chiamati «Contatori»… Il loro lavoro si basa sulla misurazione dei valori effettivi di corrente e tensione e sulla loro moltiplicazione automatica con un output di informazioni.

I contatori visualizzano il consumo di energia contando il tempo di funzionamento degli apparecchi elettrici su base incrementale dal momento in cui il contatore viene acceso sotto carico.

Per misurare la componente attiva della potenza nei circuiti CA, wattmetrie reattivo - varmetri. Hanno diverse designazioni di unità:

• watt (W, W);

• var (var, var, var).

Per determinare il consumo totale di energia, è necessario calcolarne il valore utilizzando la formula del triangolo di potenza basata sulle letture del wattmetro e del varmetro. È espresso nelle sue unità: volt-ampere.

Le designazioni accettate delle unità di ciascuna aiutano gli elettricisti a giudicare non solo il suo valore, ma anche la natura del componente di potenza.