Legge di conservazione dell'energia

La fisica moderna conosce molti tipi di energia associati al movimento o alla diversa disposizione reciproca di un'ampia varietà di corpi materiali o particelle, ad esempio, qualsiasi corpo in movimento ha un'energia cinetica proporzionale al quadrato della sua velocità. Questa energia può cambiare se la velocità del corpo aumenta o diminuisce. Un corpo sollevato dal suolo ha un'energia potenziale gravitazionale che varia tre variazioni dell'altezza del corpo.

Le cariche elettriche stazionarie che si trovano a una certa distanza l'una dall'altra hanno un'energia potenziale elettrostatica in accordo con il fatto che, secondo la legge di Coulomb, le cariche o si attraggono (se sono di segno diverso) o si respingono con una forza inversamente proporzionale al quadrato di la distanza tra loro.

L'energia cinetica e potenziale è posseduta da molecole, atomi e particelle, i loro costituenti - elettroni, protoni, neutroni, ecc. sotto forma di lavoro meccanico, nel flusso di corrente elettrica, nel trasferimento di calore, nel cambiamento dello stato interno dei corpi, nella propagazione di onde elettromagnetiche, ecc.

Più di 100 anni fa è stata stabilita una legge fondamentale della fisica, secondo la quale l'energia non può scomparire o sorgere dal nulla. Può solo passare da un tipo all'altro…. Questa legge è chiamata legge di conservazione dell'energia.

Nelle opere di A. Einstein, questa legge è notevolmente sviluppata. Einstein stabilì l'intercambiabilità di energia e massa e in tal modo ampliò l'interpretazione della legge di conservazione dell'energia, che ora è comunemente indicata come legge di conservazione dell'energia e della massa.

In accordo con la teoria di Einstein, qualsiasi variazione dell'energia dE del corpo è correlata a una variazione della sua massa dm mediante la formula dE =dmc2, dove c è la velocità della luce nel vuoto pari a 3 x 108 Miss.

Da questa formula, in particolare, segue che se, a seguito di qualche processo, la massa di tutti i corpi coinvolti nel processo diminuisce di 1 g, allora l'energia pari a 9×1013 J, che equivale a 3000 tonnellate di carburante normale.

Questi rapporti sono di primaria importanza nell'analisi delle trasformazioni nucleari. Nella maggior parte dei processi macroscopici, la variazione di massa può essere trascurata e si può parlare solo della legge di conservazione dell'energia.

Tracciamo le trasformazioni dell'energia su qualche esempio concreto. Considera l'intera catena di conversioni di energia necessarie per produrre qualsiasi parte su un tornio (Fig. 1). Supponiamo che l'energia iniziale 1, la cui quantità assumiamo al 100%, sia ottenuta a causa della completa combustione di una certa quantità di combustibile fossile. Pertanto, per il nostro esempio, il 100% dell'energia iniziale è contenuta nei prodotti della combustione del combustibile, che sono ad alta temperatura (circa 2000 K).

I prodotti della combustione nella caldaia della centrale, una volta raffreddati, cedono la loro energia interna sotto forma di calore ad acqua e vapore acqueo. Tuttavia, per motivi tecnici ed economici, i prodotti della combustione non possono essere raffreddati a temperatura ambiente. Vengono espulsi attraverso il tubo nell'atmosfera a una temperatura di circa 400 K, portando con sé parte dell'energia originaria. Pertanto, solo il 95% dell'energia iniziale verrà trasferita all'energia interna del vapore acqueo.

Il vapore acqueo risultante entrerà nella turbina a vapore, dove la sua energia interna viene inizialmente parzialmente convertita in energia cinetica delle stringhe di vapore, che verrà poi trasmessa come energia meccanica al rotore della turbina.

Solo una parte dell'energia del vapore può essere convertita in energia meccanica. Il resto viene dato all'acqua di raffreddamento quando il vapore viene condensato nel condensatore. Nel nostro esempio, abbiamo ipotizzato che l'energia trasferita al rotore della turbina sarebbe stata di circa il 38%, che corrisponde all'incirca allo stato delle cose nelle moderne centrali elettriche.

Quando si converte l'energia meccanica in energia elettrica a causa del cosiddetto Le perdite di Joule negli avvolgimenti del rotore e dello statore del generatore perderanno circa il 2% dell'energia. Di conseguenza, circa il 36% dell'energia iniziale andrà in rete.

Un motore elettrico convertirà solo una parte dell'energia elettrica fornitagli in energia meccanica per far ruotare il tornio. Nel nostro esempio, circa il 9% dell'energia sotto forma di calore Joule negli avvolgimenti del motore e calore di attrito nei suoi cuscinetti verrà rilasciato nell'atmosfera circostante.

Pertanto, solo il 27% dell'energia iniziale verrà erogata agli organi di lavoro della macchina. Ma anche i contrattempi energetici non finiscono qui. Si scopre che la maggior parte dell'energia durante la lavorazione di un pezzo viene spesa per attrito e sotto forma di calore viene rimossa con il liquido che raffredda il pezzo. Teoricamente, solo una piccolissima frazione (nel nostro esempio si assume il 2%) dell'energia iniziale sarebbe sufficiente per ottenere la parte desiderata della parte originaria.

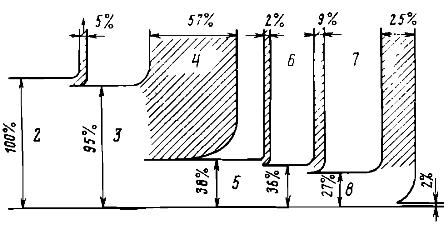
Riso. 1. Diagramma delle trasformazioni di energia durante la lavorazione di un pezzo su un tornio: 1 - perdita di energia con gas di scarico, 2 - energia interna dei prodotti della combustione, 3 - energia interna del fluido di lavoro - vapore acqueo, 4 - calore rilasciato dal raffreddamento acqua in un condensatore a turbina, 5 - energia meccanica del rotore di un generatore a turbina, 6 - perdite nel generatore elettrico, 7 - spreco nell'azionamento elettrico della macchina, 8 - energia meccanica di rotazione della macchina, 9 - attrito lavoro, che viene convertito in calore, separato dal liquido, la parte di raffreddamento, 10 - aumentando l'energia interna della parte e dei trucioli dopo l'elaborazione ...

Dall'esempio considerato, se lo si considera abbastanza tipico, si possono trarre almeno tre conclusioni molto utili.

In primo luogo, ad ogni fase della conversione dell'energia, una parte di essa viene persa... Questa affermazione non deve essere intesa come una violazione della legge di conservazione dell'energia. Si perde a causa dell'effetto utile per il quale viene eseguita la trasformazione corrispondente. La quantità totale di energia dopo la conversione rimane invariata.

Se il processo di conversione e trasferimento di energia avviene in una determinata macchina o apparato, l'efficienza di questo dispositivo è solitamente caratterizzata da efficienza (efficienza)... Uno schema di tale dispositivo è mostrato in fig. 2.

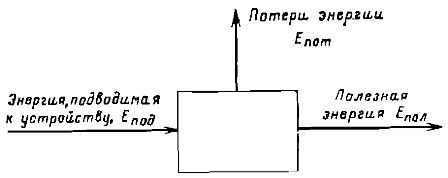
Riso. 2. Schema per determinare l'efficienza di un dispositivo che converte l'energia.

Utilizzando la notazione mostrata in figura, l'efficienza può essere definita come Efficienza = Epol/Epod

È chiaro che in questo caso, in base alla legge di conservazione dell'energia, deve esserci Epod = Epol + Epot

Pertanto, l'efficienza può anche essere scritta come segue: efficienza = 1 — (Epot / Epol)

Ritornando all'esempio mostrato in FIG. 1, possiamo dire che l'efficienza della caldaia è del 95%, l'efficienza di conversione dell'energia interna del vapore in lavoro meccanico è del 40%, l'efficienza del generatore elettrico è del 95%, l'efficienza è - l'azionamento elettrico di un macchina - 75% e l'efficienza dell'effettiva lavorazione del pezzo è di circa il 7%.

In passato, quando le leggi della trasformazione dell'energia non erano ancora note, il sogno delle persone era quello di creare una cosiddetta macchina a moto perpetuo, un dispositivo che avrebbe svolto un lavoro utile senza spendere energia. Un tale ipotetico motore, la cui esistenza violerebbe la legge di conservazione dell'energia, è oggi chiamato macchina a moto perpetuo del primo tipo, in contrapposizione a macchina a moto perpetuo del secondo tipo. seriamente la possibilità di creare una macchina a moto perpetuo del primo tipo.

In secondo luogo, tutte le perdite di energia vengono infine convertite in calore, che viene rilasciato nell'aria atmosferica o nell'acqua dai serbatoi naturali.

In terzo luogo, le persone finiscono per utilizzare solo una piccola frazione dell'energia primaria che viene spesa per ottenere il relativo effetto benefico.

Ciò è particolarmente evidente se si guarda ai costi di trasporto dell'energia. Nella meccanica idealizzata, che non considera le forze di attrito, i carichi in movimento sul piano orizzontale non richiedono energia.

In condizioni reali, tutta l'energia consumata da un veicolo viene utilizzata per vincere le forze di attrito e le forze di resistenza dell'aria, ovvero, in ultima analisi, tutta l'energia consumata nel trasporto viene convertita in calore. A questo proposito, sono interessanti le seguenti cifre che caratterizzano il lavoro di spostamento di 1 tonnellata di carico a una distanza di 1 km con diversi tipi di trasporto: aereo - 7,6 kWh / (t-km), auto - 0,51 kWh / ( t- km) , treno-0,12 kWh / (t-km).

Pertanto, lo stesso effetto benefico può essere ottenuto con il trasporto aereo a scapito di un consumo energetico 60 volte maggiore rispetto al trasporto ferroviario. Naturalmente, un elevato consumo di energia consente un notevole risparmio di tempo, ma anche a parità di velocità (auto e treno), i costi energetici differiscono di 4 volte.

Questo esempio suggerisce che le persone spesso scendono a compromessi con l'efficienza energetica per raggiungere altri obiettivi, ad esempio comfort, velocità, ecc. le valutazioni economiche dell'efficienza dei processi sono importanti... Ma all'aumentare del prezzo delle componenti energetiche primarie, la componente energetica nelle valutazioni tecniche ed economiche diventa sempre più importante.