Alimentazione di rete trifase: attiva, reattiva, piena

I valori della potenza attiva totale e della potenza reattiva totale del circuito trifase sono pari alle somme della potenza attiva e reattiva rispettivamente per ciascuna delle tre fasi A, B e C. Questa affermazione è illustrata dalla seguente formule:

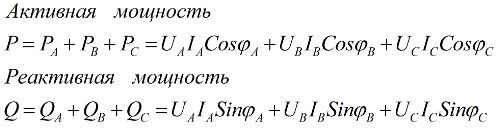
qui Ua, Ub, Uc, Ia, Ib, Ic sono i valori delle tensioni e delle correnti di fase e φ è lo sfasamento.

Quando il carico è simmetrico, cioè in condizioni in cui la potenza attiva e reattiva di ciascuna delle fasi sono uguali tra loro, per trovare la potenza totale del circuito multifase è sufficiente moltiplicare il valore della potenza di fase per il numero di fasi coinvolte. La potenza totale è determinata in base ai valori ottenuti dei suoi componenti attivi e reattivi:

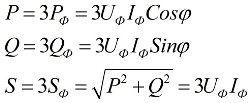
Nelle formule di cui sopra, i valori di fase delle grandezze possono essere espressi in termini dei loro valori lineari, che differiranno per gli schemi di connessione a stella oa triangolo per gli utenti, ma le formule di potenza alla fine saranno le stesse:

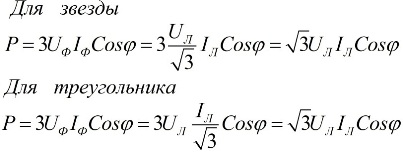
Dalle espressioni precedenti risulta che indipendentemente dallo schema di connessione dei ricevitori di energia elettrica, sia esso un triangolo o una stella, se il carico è simmetrico, le formule per trovare la potenza avranno la stessa forma, sia per un triangolo e per una stella:

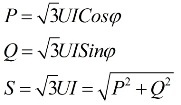
Queste formule mostrano valori lineari di tensione e corrente e sono scritte senza pedici. Di solito si trova una tale notazione, senza pedici, cioè se non ci sono pedici, allora intendiamo valori lineari.

Uno speciale dispositivo di misurazione, chiamato wattmetro… Le sue letture sono determinate dalla formula:

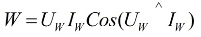
nella formula precedente, Uw e Iw sono i vettori della tensione applicata al carico e della corrente che lo attraversa.

La natura del carico attivo e lo schema di collegamento di fase possono essere diversi, pertanto, a seconda delle circostanze specifiche, gli schemi di collegamento del wattmetro saranno diversi.

Per circuiti trifase caricati simmetricamente, per una misura approssimativa della potenza attiva totale, se non è richiesta un'elevata precisione, è sufficiente un wattmetro collegato a una sola delle fasi. Dopodiché, per ottenere il valore della potenza attiva dell'intero circuito, resta da moltiplicare le letture del wattmetro per il numero di fasi:

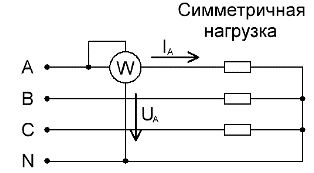
Per un circuito a quattro fili con filo neutro, per misurare con precisione la potenza attiva, sono necessari tre wattmetri, ciascuno dei quali viene letto e poi sommato per ottenere un valore per la potenza totale del circuito:

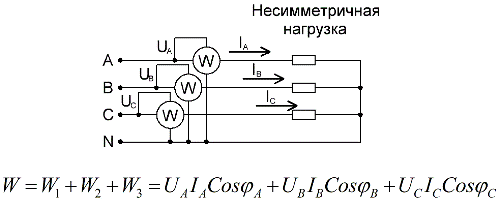
Se non è presente un filo neutro in un circuito trifase, sono sufficienti due wattmetri per misurare la potenza totale, anche se il carico è sbilanciato.

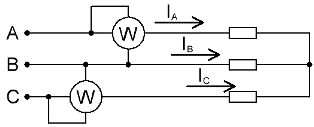
In assenza di un conduttore neutro, le correnti di fase sono interconnesse secondo la prima legge di Kirchhoff:

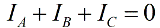
Quindi la somma delle letture di una coppia di wattmetri sarà pari a:

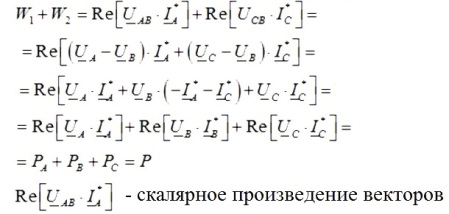
Quindi, se si aggiungono le letture di una coppia di wattmetri, si ottiene la potenza attiva totale nel circuito trifase in esame, e le letture dei wattmetri dipenderanno sia dalla dimensione del carico che dalla sua natura.

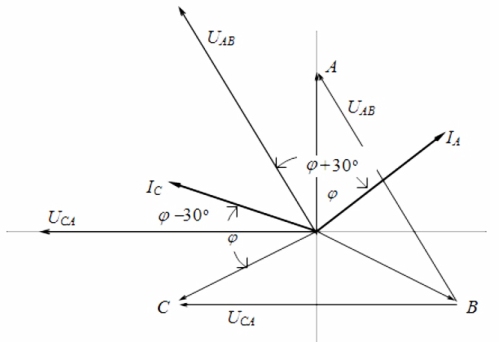
Osservando il diagramma vettoriale di correnti e tensioni in connessione con un carico simmetrico, si può concludere che le letture dei wattmetri sono determinate dalle seguenti formule:

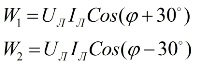
Dopo aver analizzato queste espressioni, si può capire che con un carico puramente attivo, quando φ = 0, le letture dei due wattmetri saranno uguali tra loro, cioè W1 = W2.

Con induttanza di carico attiva, quando 0 ≤ φ ≤ 90 °, le letture del wattmetro 1 saranno inferiori a quelle del wattmetro 2, cioè W1 60 °, le letture del wattmetro 1 saranno negative, cioè W1 <0.

Con una natura attiva-capacitiva del carico, quando 0 ≥ φ≥ -90 °, le letture del wattmetro 2 saranno inferiori al wattmetro 1, ovvero W1> W2. A φ <-60 °, le letture del wattmetro 2 diventeranno negative.