Legge di Ohm per un circuito magnetico

Se non ci fossero flussi magnetici, è improbabile che esisterebbe la moderna ingegneria elettrica. Il funzionamento di generatori e motori elettrici, elettromagneti e trasformatori, strumenti di misura e sensori Hall si basa sull'utilizzo del campo magnetico e sulle proprietà del flusso magnetico.

Per concentrare e rafforzare il flusso magnetico, ricorrono all'uso di materiali ferromagnetici. Vengono prodotti materiali ferromagnetici nuclei magnetici - corpi delle forme e delle dimensioni richieste, nuclei per dirigere flussi magnetici di una o dell'altra dimensione nella direzione richiesta. Tali corpi, all'interno dei quali passano linee chiuse di induzione magnetica, sono chiamati circuiti magnetici.

Le proprietà note del campo magnetico consentono di calcolare i flussi magnetici in vari circuiti magnetici. Ma per il lavoro pratico è molto più conveniente ricorrere alle conseguenze generali e alle leggi dei circuiti magnetici derivate dalle leggi del campo magnetico, invece di utilizzare direttamente queste leggi ogni volta. L'applicazione di determinate regole ai circuiti magnetici è più conveniente per risolvere problemi pratici tipici.

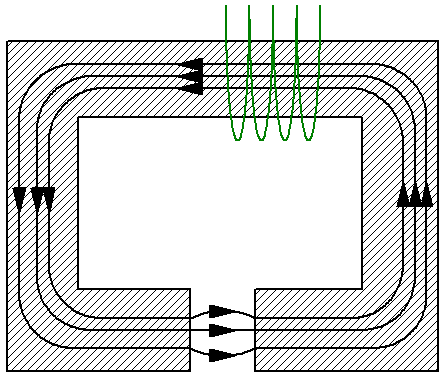
Ad esempio, si consideri un semplice circuito magnetico costituito da un giogo non ramificato di sezione trasversale S, che a sua volta è costituito da un materiale con permeabilità mu… Il giogo ha un traferro non magnetico della stessa area S, ad esempio aria, e la permeabilità magnetica nel traferro — mu1 — è diversa dalla permeabilità magnetica del giogo. Qui puoi guardare la linea media di induzione e applicarvi il teorema della tensione magnetica:

Poiché le linee di induzione magnetica sono continue in tutto il circuito, l'intensità del flusso magnetico sia nel giogo che nel traferro è la stessa. Ora usiamo le formule per induzione magnetica B e per il flusso magnetico F per esprimere l'intensità H del campo magnetico in termini di flusso magnetico F.

Il passo successivo è sostituire le espressioni risultanti nella formula precedente del teorema del flusso magnetico:

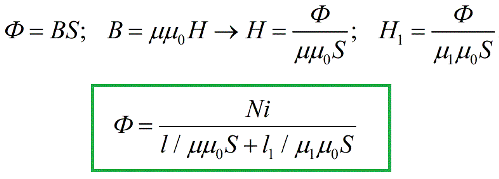
Abbiamo ottenuto una formula molto simile a quella nota in ingegneria elettrica Legge di Ohm per una sezione di un circuito chiuso, e il ruolo dell'EMF qui è svolto dalla quantità iN, chiamata forza magnetomotrice (o MDF) per analogia con la forza elettromotrice. Nel sistema SI, la forza magnetomotrice è misurata in ampere.

La somma nel denominatore non è altro che un'analogia della resistenza elettrica totale per un circuito elettrico, e per un circuito magnetico è chiamata di conseguenza la resistenza magnetica totale. I termini al denominatore sono le resistenze magnetiche delle singole sezioni del circuito magnetico.

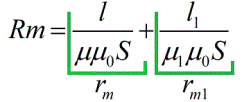
Le resistenze magnetiche dipendono dalla lunghezza del circuito magnetico, dalla sua area della sezione trasversale e dalla permeabilità magnetica (simile alla conducibilità elettrica per la solita legge di Ohm).Di conseguenza, puoi scrivere la formula della legge di Ohm, solo per un circuito magnetico:

Cioè, la formulazione della legge di Ohm in relazione a un circuito magnetico suona così: «in un circuito magnetico senza ramificazioni, il flusso magnetico è uguale al quoziente della divisione di MDS per la resistenza magnetica totale del circuito.»

È ovvio dalle formule che la resistenza magnetica in NE si misura in weber ampere, e la resistenza magnetica totale di un circuito magnetico è numericamente uguale alla somma delle resistenze magnetiche delle parti di quel circuito magnetico.

La situazione descritta è valida per un circuito magnetico non ramificato che includa un numero qualsiasi di parti, a condizione che il flusso magnetico penetri successivamente in tutte queste parti. Se i nuclei magnetici sono collegati in serie, la resistenza magnetica totale si trova sommando le resistenze magnetiche delle parti.

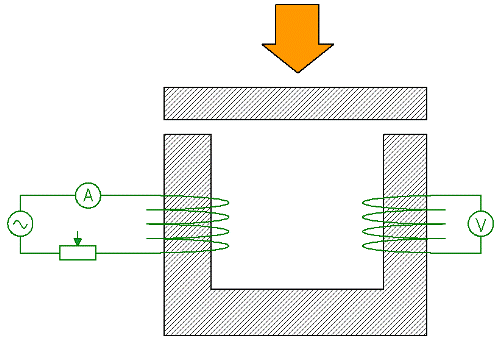
Consideriamo ora un esperimento che dimostri l'effetto della riluttanza di parti di un circuito sulla riluttanza totale di un circuito: un circuito magnetico a forma di U è magnetizzato dalla bobina 1, che è alimentata (corrente alternata) attraverso un amperometro e un reostato. Un EMF viene indotto nell'avvolgimento secondario 2 e le letture del voltmetro collegato all'avvolgimento, come sapete, sono proporzionali al flusso magnetico nel circuito magnetico.

Se ora si mantiene inalterata la corrente nell'avvolgimento primario regolandola con un reostato, e contemporaneamente si preme la piastra di ferro contro il circuito magnetico sovrastante, dopo che la resistenza magnetica totale del circuito si sarà notevolmente ridotta, la lettura della il voltmetro aumenterà di conseguenza.

Naturalmente, i termini di cui sopra, come "magnetoreresistenza" e "forza magnetomotrice", sono concetti formali, poiché nulla nel flusso magnetico si muove, non ci sono particelle in movimento, è solo una rappresentazione visiva (come un modello di flusso fluido) di una comprensione più chiara delle leggi...

Il significato fisico dell'esperimento di cui sopra e di altri esperimenti simili è capire come l'introduzione di spazi non magnetici e materiali magnetici nel circuito magnetico influenzi il flusso magnetico nel circuito magnetico.

Introducendo, ad esempio, un magnete in un circuito magnetico, aggiungiamo ulteriori correnti molecolari ai corpi già contenuti nel circuito, che introducono ulteriori flussi magnetici. Concetti formali come «resistenza magnetica» e «forza magnetomotrice» si rivelano molto convenienti quando si risolve un problema pratico, motivo per cui vengono utilizzati con successo nell'ingegneria elettrica.