Effetto di superficie ed effetto di prossimità

La resistenza del conduttore alla corrente continua è determinata dalla nota formula ro =ρl / S.

Questa resistenza può anche essere determinata conoscendo l'entità della corrente costante IО e la potenza PO:

ro = PO / AzO2

Si scopre che in un circuito a corrente alternata, la resistenza r dello stesso conduttore è maggiore della resistenza costantecorrente: r> rО

Questa resistenza r in contrasto con la resistenza in corrente continua rO ed è chiamata resistenza attiva. L'aumento della resistenza del filo è spiegato dal fatto che con la corrente alternata, la densità di corrente non è la stessa in punti diversi della sezione trasversale del filo. Ho superfici conduttrici, la densità di corrente è maggiore rispetto alla corrente continua e il centro è più piccolo.

Ad alta frequenza, le irregolarità appaiono così nitide che la densità di corrente in una significativa purezza centrale della sezione trasversale del conduttore è praticamente zero., la corrente passa solo nello strato superficiale, motivo per cui questo fenomeno è chiamato effetto superficiale.

Pertanto, l'effetto di superficie porta ad una riduzione della sezione del conduttore attraversato dalla corrente (sezione attiva), e quindi ad un aumento della sua resistenza rispetto alla resistenza in corrente continua.

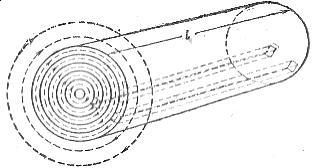
Per spiegare la causa dell'effetto superficie, si immagini un conduttore cilindrico (Fig. 1), costituito da un gran numero di conduttori elementari della stessa sezione, molto vicini tra loro e disposti in strati concentrici.

Le resistenze di questi fili alla corrente continua, rilevate dalla formula ρl / S, saranno le stesse.

Riso. 1. Il campo magnetico di un conduttore cilindrico.

Una corrente elettrica alternata crea un campo magnetico alternato attorno a ciascun filo (Fig. 1). Ovviamente, il conduttore elementare posto più vicino all'asse è circondato da un conduttore superficiale di grande flusso magnetico, quindi il primo ha un'induttanza e una reattanza induttiva più elevate del secondo.

A parità di tensione ai capi dei fili elementari di lunghezza l posti lungo l'asse e sulla superficie, la densità di corrente nel primo è minore che nel secondo.

Differenza v la densità di corrente lungo l'asse e lungo la periferia del conduttore aumenta con un aumento del diametro del conduttore d, della conduttività del materiale γ, della permeabilità magnetica del materiale μ e della frequenza AC.

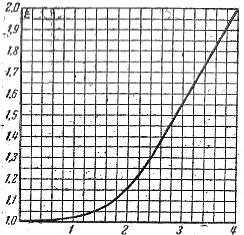
Il rapporto tra la resistenza attiva di un conduttore r e la sua resistenza a. la corrente continua rО è chiamata coefficiente di effetto pelle ed è indicata dalla lettera ξ (xi), pertanto il coefficiente ξ può essere determinato dal grafico in fig. 2, che mostra la dipendenza di ξ dal prodotto d e √γμμое.

Riso. 2. Grafico per la determinazione del coefficiente di effetto pelle.

Nel calcolare questo prodotto, d dovrebbe essere espresso in cm, γ — in 1 / ohm-cm, μo — v gn/ cm e f = in Hz.

Un esempio. È necessario determinare il coefficiente dell'effetto pelle per I sono un conduttore di rame con un diametro di d= 11,3 mm (S = 100 mm2) a una frequenza di f = 150 Hz.

Buon lavoro.

Secondo il grafico di fig. 2 troviamo ξ = 1.03

La densità di corrente disuguale in un conduttore si verifica anche a causa dell'influenza delle correnti nei conduttori vicini. Questo fenomeno è chiamato effetto di prossimità.

Considerando il campo magnetico delle correnti nella stessa direzione in due conduttori paralleli, è facile dimostrare che quei conduttori elementari appartenenti a conduttori diversi, che sono più distanti tra loro, sono collegati con il flusso magnetico più piccolo, quindi la densità di corrente in essi è il più alto. Se le correnti nei fili paralleli hanno direzioni diverse, si può dimostrare che si osserva un'elevata densità di corrente in quei fili elementari appartenenti a fili diversi che sono più vicini tra loro.