Rigidità dielettrica dell'isolamento. Esempi di calcolo

Con un aumento graduale della tensione U tra conduttori separati da un dielettrico (isolamento), ad esempio piastre di condensatori o fili conduttori di cavi, l'intensità (forza) del campo elettrico nel dielettrico aumenta. Anche l'intensità del campo elettrico nel dielettrico aumenta al diminuire della distanza tra i fili.

A una certa intensità di campo, si verifica un guasto nel dielettrico, si forma una scintilla o un arco e nel circuito appare una corrente elettrica. L'intensità del campo elettrico in cui si verifica la rottura dell'isolamento è chiamata resistenza elettrica Epr dell'isolamento.

La rigidità dielettrica è definita come tensione per mm di spessore dell'isolamento ed è misurata in V/mm (kV/mm) o kV/cm. Ad esempio, la rigidità dielettrica dell'aria tra piastre lisce è di 32 kV / cm.

La forza del campo elettrico in un dielettrico per il caso in cui i conduttori sono sotto forma di piastre o strisce separate da uno spazio uguale (ad esempio, in un condensatore di carta) è calcolata dalla formula

E = U / d,

dove U è la tensione tra i fili, V (kV); d — spessore dello strato dielettrico, mm (cm).

Esempi di

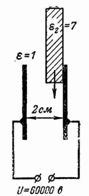
1. Qual è l'intensità del campo elettrico nel traferro di 3 cm di spessore tra le piastre se la tensione tra di esse è U = 100 kV (Fig. 1)?

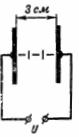
Riso. 1.

L'intensità del campo elettrico è: E = U / d = 100000/3 = 33333 V / cm.

Tale tensione supera la rigidità dielettrica dell'aria (32 kV / cm) e sussiste il rischio di distruzione.

Il rischio di danni alla corrente continua può essere prevenuto aumentando la distanza, ad esempio, a 5 cm, o utilizzando un altro isolamento più resistente invece dell'aria, come il cartone elettrico (Fig. 2).

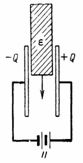
Riso. 2.

Il cartone elettrico ha una costante dielettrica di ε = 2 e una rigidità dielettrica di 80.000 V/cm. Nel nostro caso l'intensità del campo elettrico nell'isolante è di 33333 V. L'aria non può sopportare questa forza, mentre il quadro elettrico in questo caso ha una riserva di rigidità dielettrica di 80.000/33333 = 2,4, poiché la rigidità dielettrica del quadro elettrico è 80.000/32.000 = 2,5 volte quello dell'aria.

2. Qual è l'intensità del campo elettrico nel dielettrico di un condensatore di 3 mm di spessore se il condensatore è collegato a una tensione U = 6 kV?

E = U / d = 6000 / 0,3 = 20000 V / cm.

3. Un dielettrico con uno spessore di 2 mm si rompe a una tensione di 30 kV. Qual era la sua forza elettrica?

E = U / d = 30.000 / 0,2 = 150.000 V / cm = 150 kV / cm. Il vetro ha una tale forza elettrica.

4. Lo spazio tra le piastre del condensatore è riempito con strati di cartone elettrico e uno strato di mica dello stesso spessore (Fig. 3). La tensione tra le armature del condensatore è U = 10000 V. Il cartone elettrico ha una costante dielettrica ε1 = 2 e mica ε2 = 8.Come sarà distribuita la tensione U tra gli strati di isolamento e che intensità avrà il campo elettrico nei singoli strati?

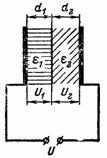
Riso. 3.

Le tensioni U1 e U2 attraverso strati dielettrici dello stesso spessore non saranno uguali. La tensione del condensatore sarà divisa in tensioni U1 e U2, che saranno inversamente proporzionali alle costanti dielettriche:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2.

Poiché U = U1 + U2, abbiamo due equazioni in due incognite.

Sostituisci la prima equazione nella seconda: U = 4 ∙ U2 + U2 = 5 ∙ U2.

Pertanto, 10000 V = 5 ∙ U2; U2 = 2000V; U1 = 4, U2 = 8000V.

Sebbene gli strati dielettrici abbiano lo stesso spessore, non sono ugualmente carichi. Un dielettrico con una costante dielettrica più alta è meno caricato (U2 = 2000 V) e viceversa (U1 = 8000 V).

L'intensità del campo elettrico E negli strati dielettrici è pari a:

E1 = U1/d1 = 8000/0,2 = 40.000 V/cm;

E2 = U2 / d2 = 2000 / 0,2 = 10000 V / cm.

La differenza nella costante dielettrica porta ad un aumento dell'intensità del campo elettrico. Se l'intero spazio fosse riempito con un solo dielettrico, ad esempio mica o cartone elettrico, l'intensità del campo elettrico sarebbe inferiore, poiché sarebbe distribuita in modo abbastanza uniforme nello spazio:

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0,4 = 25000 V / cm.

È quindi necessario evitare l'uso di isolamenti complessi con costanti dielettriche molto diverse. Per lo stesso motivo, il rischio di guasto aumenta quando si formano bolle d'aria nell'isolante.

5. Determinare l'intensità del campo elettrico nel dielettrico del condensatore dall'esempio precedente se lo spessore degli strati dielettrici non è lo stesso.Il quadro elettrico ha uno spessore d1 = 0,2 mm e mica d2 = 3,8 mm (Fig. 4).

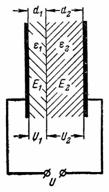
Riso. 4.

L'intensità del campo elettrico sarà distribuita in modo inversamente proporzionale alle costanti dielettriche:

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Poiché E1 = U1 / d1 = U1 / 0.2 e E2 = U2 / d2 = U2 / 3.8, allora E1 / E2 = (U1 / 0.2) / (U2 / 3.8) = (U1 ∙ 3.8) / (0.2 ∙ U2) = 19 ∙ U1 / U2.

Quindi E1 / E2 = 4 = 19 ∙ U1 / U2, ovvero U1 / U2 = 4/19.

La somma delle tensioni U1 e U2 sugli strati dielettrici è uguale alla tensione di source U: U = U1 + U2; 10000 = U1 + U2.

Poiché U1 = 4/19 ∙ U2, allora 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190.000 /23 = 8260 V; U1 = U-U2 = 1740V.

La forza del campo elettrico nella mica è E2 ∙ 8260 / 3,8≈2174 V / cm.

La mica ha una forza elettrica di 80.000 V / mm e può sopportare tale tensione.

L'intensità del campo elettrico nel quadro elettrico è E1 = 1740 / 0,2 = 8700 V / mm.

Il cartone elettrico non resisterà a tale tensione, poiché la sua rigidità dielettrica è di soli 8000 V / mm.

6. Una tensione di 60.000 V è collegata a due piastre metalliche distanti 2 cm Determinare l'intensità del campo elettrico nell'intercapedine d'aria, nonché l'intensità del campo elettrico nell'aria e nel vetro, se è presente del vetro nell'intercapedine, inserire una piastra con uno spessore di 1 cm (Fig. 5).

Riso. 5.

Se c'è solo aria tra le piastre, l'intensità del campo elettrico in essa è uguale a: E = U / d = 60.000 /2 = 30.000 V / cm.

L'intensità del campo è prossima alla rigidità dielettrica dell'aria.Se si introduce nell'intercapedine una lastra di vetro spessa 1 cm (costante dielettrica del vetro ε2 = 7), allora E1 = U1 / d1 = U1 / 1 = U1; E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60.000-U2; 8 ∙ U2 = 60.000; U2 = 7500V; E2 = U2/d2 = 7500 V/cm.

La forza del campo elettrico nel vetro è E2 = 7,5 kV / cm e la sua forza elettrica è 150 kV / cm.

In questo caso, il vetro ha un fattore di sicurezza di 20 volte.

Per il traferro si ha: U1 = 60.000-7500 = 52500 V; E1 = U1/d1 = 52500 V/cm.

In questo caso, l'intensità del campo elettrico nel traferro è maggiore che nel primo, senza vetro. Dopo aver inserito il vetro, l'intera combinazione ha meno forza della sola aria.

Il rischio di rottura si verifica anche quando lo spessore della lastra di vetro è uguale all'intercapedine tra le lastre conduttive, cioè 2 cm, poiché inevitabilmente ci saranno sottili intercapedini d'aria nell'intercapedine che verranno perforate.

La rigidità dielettrica dell'intercapedine tra i conduttori ad alta tensione deve essere rinforzata con materiali a bassa costante dielettrica e alta rigidità dielettrica, ad esempio cartone elettrico con ε = 2. Evitare combinazioni di materiali con elevata costante dielettrica (vetro , porcellana) e aria, che deve essere sostituita con olio.