Calcolo della capacità del condensatore
 La capacità C è la capacità del condensatore di accettare (immagazzinare e trattenere) la quantità di elettricità Q in ampere-secondi o la carica Q in pendenti. Se dici a un corpo, ad esempio una palla, una carica elettrica (quantità di elettricità) Q, allora un elettroscopio collegato tra questo corpo e la terra mostrerà una tensione U (Fig. 1). Questa tensione è proporzionale alla carica e dipende anche dalla forma e dalle dimensioni del corpo.
La capacità C è la capacità del condensatore di accettare (immagazzinare e trattenere) la quantità di elettricità Q in ampere-secondi o la carica Q in pendenti. Se dici a un corpo, ad esempio una palla, una carica elettrica (quantità di elettricità) Q, allora un elettroscopio collegato tra questo corpo e la terra mostrerà una tensione U (Fig. 1). Questa tensione è proporzionale alla carica e dipende anche dalla forma e dalle dimensioni del corpo.
La relazione tra carica Q e tensione U è espressa dalla formula Q = C ∙ U.
La costante di proporzionalità C si chiama capacità del corpo. Se il corpo ha la forma di una palla, la capacità del corpo è proporzionale al raggio della palla r.
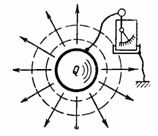
Riso. 1.
L'unità di misura della capacità è il farad (F).
Il corpo ha una capacità di 1 F quando una carica di 1 k produce una tensione di 1 V. tra esso e la terra. I farad sono un'unità di misura molto grande, quindi nella pratica vengono utilizzate unità più piccole: microfarad (μF), nanofarad (nF) e picofarad (pF)...
Queste unità sono correlate dai seguenti rapporti: 1 Ф = 10 ^ 6 μF; 1μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.
La capacità di una sfera con un raggio di 1 cm è 1,1 pF.
Non solo un corpo isolato può accumulare carica, ma anche uno speciale dispositivo chiamato condensatore. Un condensatore è costituito da due o più piastre (piastre) separate da un dielettrico (isolamento).
Nella fig. 2 mostra un circuito con una sorgente CC collegata a un condensatore. All'accensione si forma una carica positiva +Q nell'armatura destra del condensatore e una carica negativa –Q nell'armatura sinistra. Durante carica del condensatore una corrente scorre attraverso il circuito, che si interrompe dopo la fine della carica; quindi la tensione attraverso il condensatore sarà uguale a e. eccetera. c. sorgente U. La carica sulla piastra del condensatore, la tensione e la capacità sono correlate dal rapporto Q = C ∙ U. In questo caso, si forma un campo elettrostatico nel dielettrico del condensatore.
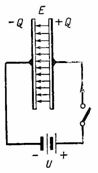
Riso. 2.
La capacità di un condensatore con un dielettrico ad aria può essere calcolata con la formula C = S / (4 ∙ π ∙ d) ∙ 1,11, pF, dove S è l'area di una piastra, cm2; d è la distanza tra le piastre, cm; C è la capacità del condensatore, pF.
La capacità di un condensatore costituito da n piastre (Fig. 3) è pari a: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1.11, pF.
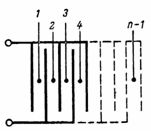
Riso. 3.
Se lo spazio tra le piastre è riempito con un altro dielettrico, ad esempio carta, la capacità del condensatore aumenterà di un fattore ε. Quando si utilizza l'isolamento in carta, la capacità aumenterà di 3 volte, con isolamento in mica - 5-8 volte, con vetro - 7 volte, ecc. Il valore di ε è chiamato costante dielettrica del dielettrico.
La formula generale per determinare la capacità di un condensatore con costante dielettrica ε (epsilon) è: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, pF.
Questa formula è utile per calcolare piccoli condensatori variabili per le radio.La stessa formula può essere rappresentata come: C = (ε_0 ∙ ε ∙ S) / d, dove ε_0 è la costante dielettrica o la costante dielettrica del vuoto (ε_0 = 8,859 ∙ 10 ^ (- 12) F / m); ε è la costante dielettrica del dielettrico.
In questa formula, le dimensioni sono sostituite in metri e la capacità è ottenuta in farad.
Esempi di
1. Qual è la capacità del pianeta Terra, il cui raggio è r = 6378 km?
Poiché la capacità di una sfera con un raggio di 1 cm è pari a 1,11 pF, la capacità della Terra è: C = 637,8 ∙ 10 ^ 6 ∙ 1,11 = 707,95 ∙ 10 ^ 6 pF = 708 μF. (La capacità di una sfera delle dimensioni del nostro pianeta è relativamente piccola. I condensatori elettrolitici di piccole dimensioni hanno questa capacità).
2. Determinare la capacità di un condensatore costituito da due piastre, ciascuna delle quali ha un'area S = 120 cm2.
Le piastre sono separate da uno strato d'aria con uno spessore di d = 0.5 cm, C = S / (4 ∙ π ∙ d) ∙ 1.11 = (120 ∙ 1.11) / (4 ∙ π ∙ 0.5) = 21 ,20 pF .. .
3. Determinare la capacità del condensatore con i dati forniti nell'esempio precedente, se lo spazio tra le piastre è riempito con carta oleata con una costante dielettrica ε = 4, vetro (ε = 7), cartone elettrico (ε = 2) , mica (ε = 8 ).
Un condensatore di carta oleata ha una capacità C = ε ∙ (S ∙ 1,11) / (4 ∙ π ∙ d) = 4 ∙ 21,2 = 84,8 pF.
La capacità di un condensatore di vetro è C = 7 ∙ 21,2 = 148,4 pF.
La capacità del condensatore di cartone è C = 2 ∙ 21,2 = 42,3 pF.
La capacità del condensatore in mica è C = 8 ∙ 21,2 = 169,6 pF.
4. Qual è la capacità di un condensatore rotante ad aria per un ricevitore radio costituito da 20 piastre con un'area di 20 cm2 se la distanza tra le piastre è di 0,06 cm (Fig. 149)?
C = (n-1) ∙ (S ∙ 1.11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1.11) / (4 ∙ π ∙ 0.06) = 559, 44 pF.
Il condensatore mostrato in Fig.3, è costituito da condensatori più semplici separati con due piastre, il cui numero è pari a n-1.
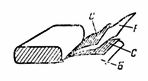
5. Un condensatore di carta di capacità C = 2 μF è costituito da due strisce di carta stagnola C e due strisce di un dielettrico di carta oleata B con una costante dielettrica ε = 6. Lo spessore della carta oleata è d = 0,1 mm. Le strisce piegate vengono arrotolate, i cavi sono ricavati dalle lastre di acciaio. Determina la lunghezza della striscia di acciaio del condensatore se la sua larghezza è di 4 cm (Fig. 4).
Riso. 4.
Innanzitutto, determiniamo l'area di una striscia con la formula C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, da cui S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = ( 2 ∙ 4 ∙ π ∙ 0,01 ∙ 10 ^ 6) / (6 ∙ 1,11); S = 2.000.000 / (6 ∙ 1,11) ∙ 4 ∙ π ∙ 0,01 = 37680 cm2.
La lunghezza di ciascuna striscia è l = 37680/4 = 9420 cm = 94,2 m.