Forza di trazione degli elettromagneti

La forza con cui un elettromagnete attrae materiali ferromagnetici dipende dal flusso magnetico F o, equivalentemente, dall'induzione B e dall'area della sezione trasversale dell'elettromagnete S.

La forza di pressione dell'elettromagnete è determinata dalla formula

FA = 40550 ∙ SI ^ 2 ∙ S,

dove F è la forza di pressione dell'elettromagnete, kg (la forza è misurata anche in newton, 1 kg = 9,81 N o 1 N = 0,102 kg); B — induzione, T; S è l'area della sezione trasversale dell'elettromagnete, m2.

Esempi di

1. L'elettromagnete del rubinetto è un circuito magnetico (Fig. 1). Qual è la forza di sollevamento di un elettromagnete per gru a ferro di cavallo, se l'induzione magnetica è B = 1 T e l'area della sezione trasversale di ciascun polo dell'elettromagnete è S = 0,02 m2 (Fig. 1, b)? Trascurare l'effetto dello spazio tra l'elettromagnete e l'armatura.

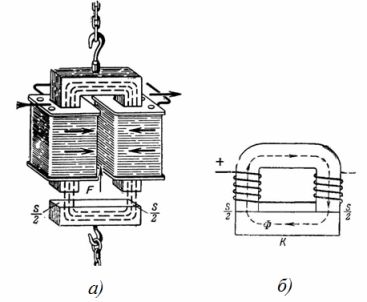
Riso. 1. Elettromagnete di sollevamento

F = 40550 ∙ SI ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0,02 = 1622 kg.

2. Un elettromagnete circolare in acciaio ha le dimensioni indicate in fig. 2, a e b. La forza di sollevamento dell'elettromagnete è 3 T. Determina l'area della sezione trasversale del nucleo dell'elettromagnete, n. p. e il numero di spire della bobina a una corrente di magnetizzazione I = 0,5 A.

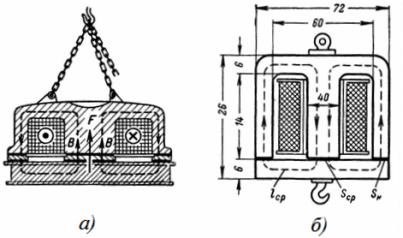
Riso. 2. Elettromagnete rotondo

Il flusso magnetico passa attraverso il nucleo interno circolare e ritorna attraverso il corpo cilindrico. Le sezioni trasversali del nucleo Sc e dell'involucro Sk sono approssimativamente le stesse, quindi i valori di induzione nel nucleo e nell'involucro sono praticamente gli stessi:

Sc = (π ∙ 40 ^ 2) / 4 = (3,14 ∙ 1600) / 4 = 1256 cm2 = 0,1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3,14 / 4 ∙ (5184-3600) = 1243,5 cm2 = 0,12435 m2;

S = Sc + Sk = 0,24995 m2 ≈0,25 m2.

L'induzione richiesta nell'elettromagnete è determinata dalla formula F = 40550 ∙ B ^ 2 ∙ S,

dove B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0,25)) = 0,5475 T.

La tensione a questa induzione si trova sulla curva di magnetizzazione dell'acciaio fuso:

H = 180 A/m.

La lunghezza media della linea di campo (Fig. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0,86 m.

Forza di magnetizzazione I ∙ ω = H ∙ lav = 180 ∙ 0,86 = 154,8 Av; io = (io ∙ ω) / io = 154,8 / 0,5 = 310 A.

In realtà n. s, cioè la corrente e il numero di giri, devono essere molte volte maggiori, poiché tra l'elettromagnete e l'armatura c'è un inevitabile traferro, che aumenta notevolmente la resistenza magnetica del circuito magnetico. Pertanto, il traferro deve essere preso in considerazione nel calcolo degli elettromagneti.

3. La bobina dell'elettromagnete per il rubinetto ha 1350 giri, attraverso di essa scorre una corrente I = 12 A. Le dimensioni dell'elettromagnete sono mostrate in fig. 3. Quale peso solleva l'elettromagnete a una distanza di 1 cm dall'armatura e quale peso può sostenere dopo la gravità?

Riso. 3. Bobina elettromagnetica

La maggior parte di N. con I ∙ ω viene spesa per condurre il flusso magnetico attraverso il traferro: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Forza di magnetizzazione I ∙ ω = 12 ∙ 1350 = 16200 A.

Poiché H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, allora Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02.

Pertanto, 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0,02, cioè B = 1.012 T.

Supponiamo che l'induzione sia B = 1 T, poiché parte di n. c. I ∙ ω è speso per condurre il flusso magnetico nell'acciaio.

Controlliamo questo calcolo con la formula I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

La lunghezza media della linea magnetica è: lav = 2 ∙ (7 + 15) = 44 cm = 0,44 m.

L'intensità Hc a B = 1 T (10000 Gs) è determinata dalla curva di magnetizzazione:

Hc = 260 A / m.I ∙ ω = 0,8 ∙ B ∙ 2 + 2,6 ∙ 44 = 1,6 ∙ 10000 + 114,4 = 16114 Av.

La forza magnetizzante I ∙ ω = 16114 Av che crea un'induzione B = 1 T è praticamente uguale al dato n. v. io ∙ ω = 16200 Av.

L'area della sezione trasversale totale del nucleo e del cono è: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0,006 m2.

L'elettromagnete attirerà una carica di peso F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0,006 = 243,3 kg da una distanza di 1 cm.

Poiché il traferro praticamente scompare dopo che l'armatura è stata attratta, l'elettromagnete può sopportare un carico molto maggiore. In questo caso, l'intero n. c) I ∙ ω è speso per condurre il flusso magnetico solo nell'acciaio, quindi I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

A tale tensione, l'acciaio è praticamente saturo e l'induzione in esso è di circa 2 T. L'elettromagnete attrae l'armatura con una forza F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0,006 = 973 kg.

4. Il relè di segnale (lampeggiante) è costituito da un elettromagnete corazzato 1 con un nucleo tondo e un'armatura a valvola 2, che, dopo aver fornito corrente all'elettromagnete, attrae e rilascia il lampeggiante 3, che apre la cifra del segnale (Fig. 4).

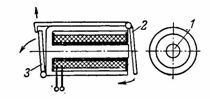
Riso. 4. Elettromagnete dell'armatura

La forza magnetizzante è I ∙ ω = 120 Av, il traferro è δ = 0,1 cm e l'area della sezione trasversale totale dell'elettromagnete è S = 2 cm2. Stimare la forza di trazione del relè.

L'induttanza B è determinata per approssimazioni successive usando l'equazione I ∙ ω = Hñ ∙ lñ + Hδ ∙ 2 ∙ δ.

Sia n. c. Hc ∙ lc è 15% I ∙ ω, cioè 18 Av.

Allora I ∙ ω-Hñ ∙ lñ = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0,2; Hδ = 102 / 0,2 = 510 A / cm = 51000 A / m.

Quindi troviamo l'induzione B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0,0637 T.

Dopo aver sostituito il valore B nella formula F = 40550 ∙ B ^ 2 ∙ S, otteniamo:

F = 40550 ∙ 0,0637 ^ 2 ∙ 0,0002 = 0,0326 kg.

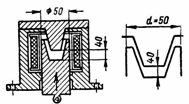
5. L'elettrovalvola del freno CC (Fig. 5) ha un'armatura del pistone con un arresto conico. La distanza tra l'armatura e l'anima è di cm 4. Il diametro di lavoro (anime con area di contatto circolare) d = 50 mm. L'armatura viene tirata nella bobina con una forza di 50 kg. La lunghezza della linea mediana di forza lav = 40 cm Determinare n. pp. e la corrente della bobina se ci sono 3000 spire.

Riso. 5. Solenoide del freno CC

L'area della sezione di lavoro dell'elettromagnete è uguale all'area di un cerchio con un diametro d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3,14 / 4 ∙ 25 = 19,6 cm2.

L'induzione B richiesta per creare una forza F = 50 kg si trova dall'equazione F = 40550 ∙ B ^ 2 ∙ S,

dove B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0,00196)) = 0,795 T.

Forza magnetizzante I ∙ ω = Hñ ∙ lñ + Hδ ∙ δ.

Determiniamo la forza magnetizzante per l'acciaio Hc ∙ lc in modo semplificato, basandoci sul fatto che è 15% I ∙ ω:

io ∙ ω = 0,15 ∙ io ∙ ω + Hδ ∙ δ; 0,85 ∙ io ∙ ω = Hδ ∙ δ; 0,85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; io ∙ ω = (8 ∙ 10 ^ 5 ∙ 0,795 ∙ 0,04) / 0,85 = 30.000 Av.

Corrente di magnetizzazione I = (I ∙ ω) / ω = 30000/3000 = 10 A.